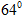Bài viết này sẽ tiếp tục hướng dẫn các em nắm được dạng bài tập tiếp theo của chương " Các định luật bảo toàn" : ÁP DỤNG ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG CHO HIỆN TƯỢNG NỔ, VA CHẠM.

Dạng 3. ÁP DỤNG ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG CHO HIỆN TƯỢNG NỔ, VA CHẠM

Phương pháp giải
 
* Sự nổ của đạn:

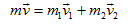
(Đạn nổ thành 2 mảnh)

(Hệ kín : Fngoại << Fnội )

Chú ý:
Trong hệ kín, các vật của hệ có thể chuyển động có gia tốc nhưng khối tâm của hệ đứng yên hoặc chuyển động thẳng đều.
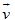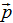Trong hiện tượng nổ, va chạm, và  có phương khác nhau -> chọn hệ trục tọa độ Oxy.
Sau khi viết phương trình vectơ của định luật và chiếu lên hệ trục tọa độ đã chọn sẽ tiến hành giải toán để suy ra các đại lượng cần tìm. Trong bước này nhiều khi có thể biểu diễn phương trình vectơ trên hình vẽ để tìm được lời giải.

Bài tập mẫu
Một viên đạn pháo đang bay ngang với vận tốc v0 = 25 m/s ở độ cao h = 80 m thì nổ, vỡ làm hai mảnh, mảnh 1 có khối lượng m1 = 2,5 kg, mảnh hai có m2 = 1,5 kg. Mảnh một bay thẳng đứng xuống dưới và rơi chạm đất với vận tốc v1’ = 90m/s. Xác điịnh độ lớn và hướng vận tốc của mảnh thứ hai ngay sau khi đạn nổ. Bỏ qua sức cản của không khí. Lấy g = 10m/s. 

Giải 
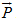
Xét hệ gồm hai mảnh. Ngoại lực tác dụng lên hệ là trọng lực  , trọng lực này không đáng kể so với lực tương tác giữa hai mảnh. Do đó hệ được coi là hệ kín. 
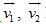
Gọi lần lượt là vận tốc của mảnh 1 và mảnh 2 ngay sau khi vỡ.
Áp dụng định luật bảo toàn động lượng cho hệ, ta có:

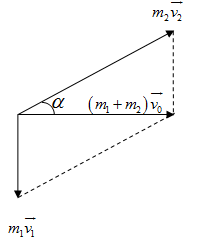
Theo đề bài: 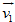   có chiều thẳng đứng hướng xuống, hướng theo phương ngang. Do đó ta có thể biểu diễn phương trình vectơ (1) như trên hình vẽ.
Theo đó:

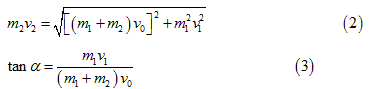
Để tính vận tốc của mảnh 1 ngay sau khi nổ ta áp dụng công thức:

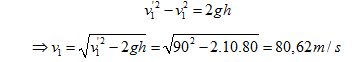
Từ (2) ta tính được:

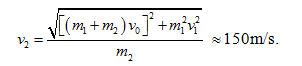
Từ (3), ta có: 

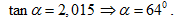
Như vậy ngay sau khi viên đạn bị vỡ, mảnh thứ 2 bay theo phương xiên lên trên hợp với phương ngang một góc