Ở bài trước, Green City Academy đã tóm tắt lại kiến thức cơ bản của chương "Các định luật bảo toàn", các dạng bài tập các em có thể gặp phải ở chương này và phương pháp giải bài tập dạng 1 - ÁP DỤNG ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG CHO HỆ KÍN.

Bài viết này sẽ tiếp tục hướng dẫn các em nắm được dạng bài tập tiếp theo: CHUYỂN ĐỘNG BẰNG PHẢN LỰC

Dạng 2. CHUYỂN ĐỘNG BẰNG PHẢN LỰC

Phương pháp giải
- Để giải các bài toán về chuyển động bằng phản lực, chỉ cần áp dụng định luật bảo toàn động lượng. Cần chú ý rằng, ban đầu hai phần của hệ có cùng vận tốc, sau đó chúng có vận tốc khác nhau (về hướng và độ lớn).
- Chuyển động của tên lửa
Trường hợp 1:
Lượng nhiên liệu cháy và phụt ra tức thời hoặc các phần của tên lửa tách rời khỏi nhau.

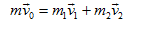
Chiếu lên phương chuyển động để thực hiện tính toán.
Nếu cần, áp dụng công thức cộng vận tốc.
Trường hợp 2:
 
Nhiên liệu cháy và phụt ra liên tục.
Áp dụng các công thức:

Bài tập mẫu
Một tên lửa khối lượng tổng cộng m = 1 tấn đang chuyển động theo phương ngang với vận tốc v = 200 m/s thì động cơ hoạt động. Từ trong tên lửa, một lượng nhiên liệu khối lượng m1 = 100 kg cháy và phụt tức thời ra phía sau với vận tốc v1= 700 m/s.
a) Tính vận tốc của tên lửa ngay sau dó.
b) Sau đó phần đuôi của tên lửa có khối lượng m¬d = 100 kg tách ra khỏi tên lửa, vẫn chuyển động theo hướng cũ với vận tốc giảm còn 1/3. Tính vận tốc phần còn lại của tên lửa.
Giải
Ta coi tên lửa như là một hệ kín khi chuyển động và xảy ra tương tác. Do đó ta hoàn toàn có thể áp dụng định luật bảo toàn động lượng.

a) Khi nhiên liệu cháy và phụt tức thời ra phía sau, vận tốc của tên lửa ngay sau đó là 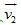 . Ta có: 

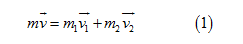
Chọn trục tọa độ Ox có chiều dương trùng với chiều chuyển động ban đầu của tên lửa (chiều của vectơ vận tốc   ).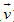
Chiếu (1) lên chiều dương đã chọn, suy ra:

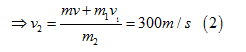
Vậy ngay sau khi nhiên liệu cháy phụt ra phía sau, tên lửa tiếp tục chuyển động theo phương cũ với vận tốc 300m/s.
b) Gọi 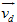  là vận tốc của đuôi tên lửa,  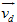cùng hướng với  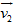và có độ lớn:

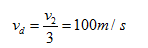
Gọi 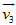  là vận tốc của phần tên lửa còn lại . Áp dụng định luật bảo toàn động lượng khi phần đuôi bị tách ra, ta có:

Với 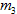  là khối lượng của phần tên lửa còn lại, và có giá trị : 

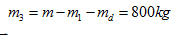
Chiếu (3) lên chiều dương theo chiều của 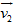 , ta có:

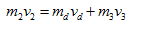
Suy ra: 

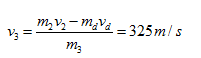
Vận tốc phần tên lửa còn lại là 325 m/s.