Kiến thức cơ bản
1. Một hệ vật gọi là hệ kín (hay cô lập) nếu các vật trong hệ chỉ tương tác với nhau mà không tương tác với các vật ở ngoài hệ (gọi tắt là môi trường ngoài).
Ví dụ: Hệ hai vật chuyển động không có ma sát trên mặt phẳng nhẵn nằm ngang. Trong các hiện tượng nổ, va chạm, hệ vật có thể coi gần đúng là hệ kín trong thời gian ngắn xảy ra hiện tượng.
2. Động lượng 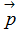 của một vật khối lượng m đang chuyển động với vận tốc
của một vật khối lượng m đang chuyển động với vận tốc 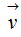 là đại lượng vectơ bằng tích của khối lượng m với vận tốc
là đại lượng vectơ bằng tích của khối lượng m với vận tốc 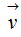 của vật:
của vật:
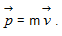
- Động lượng có hướng của vân tốc.
- Động lượng của một hệ là tổng các vectơ các động lượng của các vật trong hệ.
- Đơn vị: kg.m/s.
3. Định luật bảo toàn động lượng: Vectơ tổng động lượng của một hệ kín được bảo toàn
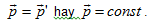
a) Đối với hệ hai vật:
.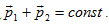
b) Nếu hệ không kín nhưng các ngoại lực có cung phương Oy chẳng hạn thì hình chiếu của tổng ngoại lực xuống phương Ox bằng không. Do đó, hình chiếu của tổng động lượng trên phương Ox vẫn bảo toàn :
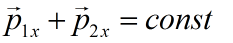
4. Liên hệ giữa lực và động lượng: Độ biến thiên động lượng của một vật trong khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó : 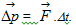
Phân loại bài tập
Dạng 1. ÁP DỤNG ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG CHO HỆ KÍN
Dạng 2. CHUYỂN ĐỘNG BẰNG PHẢN LỰC
Dạng 3. ÁP DỤNG ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG CHO HIỆN TƯỢNG NỔ, VA CHẠM
Dạng 4: TÍNH XUNG LƯỢNG CỦA LỰC
Dạng 1. ÁP DỤNG ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG CHO HỆ KÍN
Phương pháp giải
Để giải các bài tập dạng này, thông thường ta làm theo các bước như sau:
- Xác định hệ vật cần khảo sát và lập luận để thấy rằng trường hợp khảo sát hệ vật là hệ kín.
- Viết định luật dưới dạng vectơ.
- Chiếu phương trình vectơ lên phương chuyển động của vật
- Tiến hành giải toán để suy ra các đại lượng cần tìm.
Những lưu ý khi giải các bài toán liên quan đến định luật bảo toàn động lượng:
a) Trường hợp các vectơ động lượng thành phần (hay các vectơ vận tốc thành phần) cùng phương, thì biểu thức của định luật bảo toàn động lượng được viết lại:
Trong trường hợp này ta cần quy ước chiều dương của chuyển động.
- Nếu vật chuyển động theo chiều dương đã chọn thì v > 0;
- Nếu vật chuyển động ngược với chiều dương đã chọn thì v < 0.
b) Trường hợp các vectơ động lượng thành phần (hay các vectơ vận tốc thành phần) không cùng phương, thì ta cần sử dụng hệ thức vectơ:
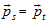
và biểu diễn trên hình vẽ. Dựa vào các tính chất hình học để tìm yêu cầu của bài toán.
Ví dụ:
Một người có khối lượng m1 = 50kg đang chạy với vận tốc v1 = 3m/s thì nhảy lên một toa tàu khối lượng m2 = 150kg chạy trên đang ray nằm ngang song song ngang qua người đó với vận tốc v2 = 2m/s. Tính vận tốc của toa tàu sau khi người đó nhảy lên, nếu ban đầu toa tàu và người chuyển động:
a) Cùng chiều
b) Ngược chiều
Giả thiết bỏ qua ma sát.
Giải
Xét hệ gồm toa xe và người. Khi người nhảy lên toa tàu với vận tốc v1. Ngoại lực tác dụng lên hệ là trọng lực 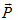 và phản lực đàn hồi
và phản lực đàn hồi 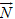 , các lực này có phương thẳng đứng. Vì các vật trong hệ chuyển động theo phương ngang nên các ngoại lực sẽ cân bằng nhau. Như vậy hệ toa xe + người được coi là hệ kín.
, các lực này có phương thẳng đứng. Vì các vật trong hệ chuyển động theo phương ngang nên các ngoại lực sẽ cân bằng nhau. Như vậy hệ toa xe + người được coi là hệ kín.
Chọn trục tọa độ Ox, chiều dương theo chiều chuyển động của toa.
Gọi v’ là vận tốc của hệ sau khi người nhảy nên xe. Áp dụng định luật bảo toàn động lượng ta có :
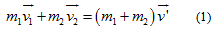
a) Trường hợp 1 : Ban đầu người và toa chuyển động cùng chiều.
Chiếu (1) lên trục Ox nằm ngang có chiều dương ta được :
Hệ tiếp tục chuyển động theo chiều cũ với vận tốc 2,25m/s.
b) Trường hợp 2 : Ban đầu người và toa chuyển động ngược chiều nhau.
Chiếu (1) lên trục Ox nằm ngang có chiều dương ta được :
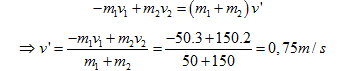
Hệ tiếp tục chuyển động theo chiều cũ với vận tốc 0,75m/s.